Fiveable SAT Math: Breaking Down the Reference Sheet

Are you finding yourself struggling to study for the math section of the SAT? Don't worry! Understanding and memorizing key formulas can give you the confidence and skills needed to tackle those math problems. In this blog, we'll break down the SAT math formulas provided in the reference sheet in a comprehensible way. So grab your notebook and let's get to it. ✍🏼

The SAT Math Reference Sheet

During the SAT, you'll be given the following reference sheet which consists of essential formulas you need to know, such as the area and perimeter of common shapes, volume of solids, special right triangle formulas, and 3 fundamental geometric rules.

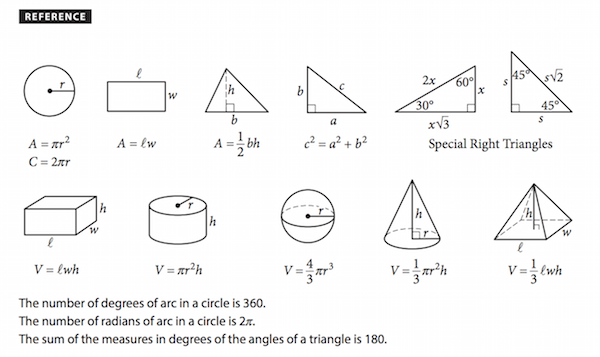
Area and Circumference of a Circle

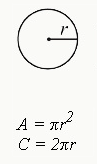
The formula of a circle is A = πr², where:  

• "A" represents the area, which is the space inside the circle,

• "π" is a special number (approximately 3.14), and

• "r" stands for the radius, which is the distance from the center of the circle to its edge. The circumference of a circle is given by C = 2πr or C = πd, where:

• "C" represents the circumference, which is the distance around the circle,

• "π" is our trusty special number (approximately 3.14),

• "r" stands for the radius,

• "d" is the diameter (the distance across the circle passing through the center). 💡You can either double the radius and multiply it by π or directly use the diameter multiplied by π to find the circumference. 

Area of a Rectangle

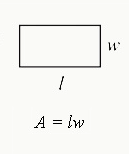
The formula for finding the area of a rectangle is A = length × width or A=lw, where:

• • "A" represents the area, which is the space inside the rectangle,
• • The "length" refers to the longer side of the rectangle, and
• • The "width" represents the shorter side. 💡To find the area, simply multiply the length by the width, and voila! ✨

Area of a Triangle

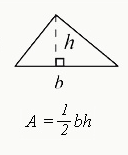
The formula for finding the area of a triangle is A = 1/2 × base × height, where:

• • "A" represents the area of the triangle,
• • The "base" refers to the length of the bottom side of the triangle, and
• • The "height" represents the perpendicular distance from the base to the top of the triangle. 💡To find the area, multiply half of the base by the height, and there you have it! 

Pythagorean Theorem

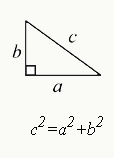
Pythagorean's theorem helps you find the unknown length of a right triangle. The theorem states that in a right triangle, the square of the length of the hypotenuse ("c") is equal to the sum of the squares of the other 2 sides ("a" and "b"). 

💡In simpler terms, it means that if you square the lengths of the 2 shorter sides ("a" and "b"), add them together, and then take the square root of that sum, you'll find the length of the hypotenuse ("c"). 

Special Right Triangles

The two most common types of special right triangles are the 45-45-90 triangle and the 30-60-90 triangle. These names come from the angles within the triangles. In a 45-45-90 triangle, both of the acute angles are 45 degrees, while in a 30-60-90 triangle, one acute angle is 30 degrees and the other is 60 degrees.

What makes these triangles special is that their side lengths follow specific ratios!

In a 45-45-90 triangle, the two legs (the sides opposite the 45-degree angles) are equal in length, and the length of the hypotenuse (the side opposite the right angle) is equal to the length of one leg multiplied by the square root of 2. 

Similarly, in a 30-60-90 triangle, the ratio of the lengths of the sides is special. The side opposite the 30-degree angle is half the length of the hypotenuse, while the side opposite the 60-degree angle is the length of the short leg multiplied by the square root of 3.

45°– 45°– 90° Triangle

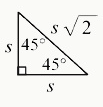
In a 45-45-90 triangle, both of the 2 shorter sides (legs) have the same length, and the length of the hypotenuse (the longest side) is equal to the length of the legs multiplied by the square root of 2. So, if you know the length of one leg in a 45-45-90 triangle, you can find the lengths of the other leg and the hypotenuse by multiplying that length by the square root of 2. 

30°- 60°- 90° Triangle

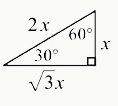
In a 30-60-90 triangle, the length of the shortest side (opposite the 30-degree angle or "x") is half the length of the hypotenuse (the longest side or "2x"). The length of the longer side (opposite the 60-degree angle) is found by multiplying the length of the shortest side by the square root of 3. And the hypotenuse is simply twice the length of the shortest side. 

Volume of a Rectangular Prism

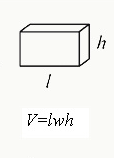
The formula for finding the volume of a rectangular prism is given by V = length × width × height, where:

• • "V" represents the volume,
• • The "length" refers to the longer dimension of the box,
• • The "width" represents the shorter dimension, and
• • The "height" is the measurement from the bottom to the top of the box. 💡To find the volume, simply multiply the length, width, and height together. 

Volume of a Cylinder

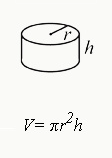
The formula for finding the volume of a cylinder is V = πr²h, where:

• • "V" represents the volume,
• • "π" is a special number (approximately 3.14),
• • "r" stands for the radius of the circular base, and
• • "h" represents the height of the cylinder. 💡To find the volume, simply square the radius, multiply it by the height, and then multiply the result by π. 

Volume of a Sphere

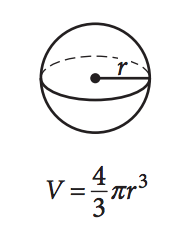
The formula for finding the volume of a sphere is V = (4/3)πr³, where:

• • "V" represents the volume,
• • "π" is a special number (approximately 3.14), and
• • "r" stands for the radius of the sphere. 💡To find the volume, cube the radius, multiply it by (4/3), and then multiply the result by π. 

Volume of a Cone

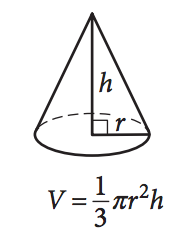
The formula for finding the volume of a cone is given by V = (1/3)πr²h, where:

• • "V" represents the volume,
• • "π" is a special number (approximately 3.14),
• • "r" stands for the radius of the circular base, and
• • "h" represents the height of the cone. 💡To find the volume, square the radius, multiply it by the height, and then multiply the result by (1/3). 

Volume of a Pyramid

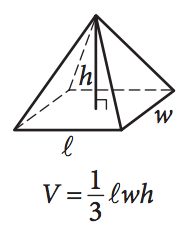
The formula for finding the volume of a pyramid, V = (1/3) × l × w × h.

"V" represents the volume. To calculate it, we need two key measurements: the base area (l × w) and the height. The "l" and "w" refers to the length and width of the base, respectively; and the "h" is the measurement from the base to the tip of the pyramid. 

💡Multiply the base area (given by multiplying the length and the width) by the height, and then multiply the result by (1/3).

💫 Conclusion

You made it to the end! Armed with these SAT math formulas and an understanding of how to use them, you are now ready to confidently tackle the math section of the SAT. Best of luck on your SAT journey, we believe in you! 🚀