What is implicit differentiation and how do I do it?

Explicit vs. Implicit Differentiation

By now, you've probably covered basic differentiation of a function y in terms of a single variable x. This is called explicit differentiation.

Implicit differentiation, on the other hand, is differentiating a variable in terms of another variable. We're not just taking the derivative of x or 8x+6 anymore, we're taking the derivative of whole equations like y = 8x+6 to find dy/dx.

Need a quick review on taking and finding derivatives, make sure you watch this 🎥 video introducing and explaining derivatives for a refresher. 

---

Explicit Differentiation

• Single variable function/relation Example:

---

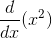
Implicit Differentiation

• More than one variable in the function/relation Example: 

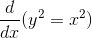
So how do you do implicit differentiation? Just apply the chain rule!

🌟 Example:

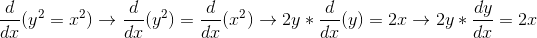
We can even simplify further to solve for dy/dx!

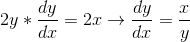
...And there you have it!

---

Implicit differentiation is useful in solving differential equations, where you'll need to solve for dy/dx. Some applications include optimization, e.g. finding the rate of change of volume with respect to the rate of change of time. 

For more examples and help watch this video about 🎥 implicit differentiation and derivatives. 

-----